Τελείωσε και η φάση των 16 ομάδων με τα αποτελέσματα να ήταν όπως αναμενόταν από το μοντέλο και από την λογική με εξαίρεση ίσως του αγώνα της Ισπανίας και Μαρόκου όπου πέρασε το τελευταίο και θεωρήθηκε έκπληξη. Το μοντέλο έπιασε 7/8 αγώνες (87.5%) και «έχασε» την πρόκριση του Μαρόκου.
Να σημειώσουμε ότι εδώ το Μαρόκο είχε μια αρκετά σημαντική πιθανότητα να φέρει τον αγώνα σε παράταση (27%) ενώ η πιθανότητα ο αγώνας να πάει παράταση ή να προκριθεί το Μαρόκο (αθροιστικά) ήταν περίπου 44%. Αυτό σημαίνει ότι αν οι δύο ομάδες έπαιζαν 4 φορές, περίπου στον 1 αγώνα θα είχαμε παράταση ενώ αν οι δύο ομάδες έπαιζαν 7 αγώνες τότε στους 3 ή θα είχαμε παράταση ή θα κέρδιζε το Μαρόκο. Συνεπώς το μοντέλο μας έλεγε ότι η Ισπανία είναι το φαβορί αλλά οι πιθανότητες να καταφέρει το Μαρόκο δεν ήταν αμελητέες.
Ένα από τα εντυπωσιακά αποτελέσματα του μοντέλου σε αυτόν τον γύρο ήταν «προέβλεψε» ότι υπάρχει ισορροπία μεταξύ Ιαπωνίας και Κροατίας, των οποίων ο αγώνας κρίθηκε στα πέναλτυ.
Οι Προβλέψεις του Μοντέλου για την Φάση των Προημιτελικών
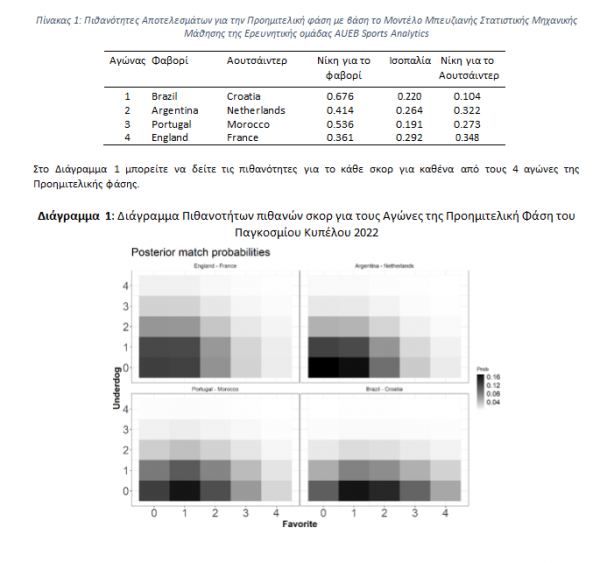
Οι ενημερωμένες προβλέψεις με τη μορφή πιθανοτήτων δίνονται στον Πίνακα 1. Ως φαβορί δηλώνεται η ομάδα με τη μεγαλύτερη πιθανότητα νίκης.
Συγκεκριμένα από τον Πίνακα 1 μόνο
· η Βραζιλία είναι ξεκάθαρο φαβορί εις βάρος της Κροατίας με πιθανότητα νίκης 67.6%
· Η Πορτογαλία έχει προβάδισμα φαβορί έναντι του Μαρόκου με πιθανότητα νίκης 53.6%. Σημείωση: ξανά το Μαρόκο έχει σημαντική πιθανότητα να τα καταφέρει: 46.4% να κερδίσει ή να πάει τον αγώνα σε παράταση και 27% να κερδίσει τον αγώνα. Άρα εικόνα παρόμοια με αυτή στον αγώνα κατά της Ισπανίας. Και το ερώτημα εδώ είναι: Μπορεί το Μαρόκο να κερδίσει τις πιθανότητες και πάλι και περάσει στα ημιτελικά;
· Η Αργεντινή έχει ελαφρύ προβάδισμα κατά της Ολλανδίας με 41.% πιθανότητα νίκης έναντι 32% για τη δεύτερη.
· Τέλος ο αγώνας Αγγλίας-Γαλλίας είναι πλήρως ισορροπημένος και όλα τα αποτελέσματα είναι πιθανά.
Προβλεπτική Ανάλυση και Σύγκριση Μοντέλων (Αυστηρά μόνο για μυημένους)
Σε αυτή την ενότητα, θα παρουσιάσουμε μια ανάλυση της προβλεπτικής απόδοσης τριών προτεινόμενων μοντέλων, που επικεντρώνονται στην μοντελοποίηση των γκολ που σημείωσαν και οι δύο αντίπαλες ομάδες, σε όλες τις αγωνιστικές ημέρες που διεξήχθησαν μέχρι το τέλος της φάσης 16 του παγκοσμίου κυπέλου (δηλαδή σε 56 αγώνες).
Τα ακόλουθα τρία μοντέλα λήφθηκαν υπόψη:
1. Διμεταβλητό Poisson με αύξηση των ισοπαλιών (Diagonal Inflated Bivariate Poisson)
2. Διμεταβλητό Poisson (Bivariate Poisson)
3. Απλό Poisson (Double Poisson)
Για την προσαρμογή αυτών των μοντέλων, χρησιμοποιήσαμε τα ίδια δεδομένα για την εκπαίδευσή τους, καθώς επίσης και το ίδιο επίπεδο πληροφορίας πριν δούμε τα δεδομένα. Το σύνολο δεδομένων για την αξιολόγηση των επιδόσεων αποτελείται από 56 αγώνες.
Για τη σύγκριση των μοντέλων χρησιμοποιήθηκε ο Μπευζιανός δείκτης LOOIC (Vehtari et al., 2017). Επιγραμματικά, αναφέρουμε ότι το LOOIC του Μοντέλου 1 ήταν το χειρότερο σε κάθε αγωνιστική ημέρα, ενώ το καλύτερο ήταν το τρίτο μοντέλο, αλλά με πολύ μικρή διαφορά σε σχέση με το Μοντέλο 2. Ως επόμενο βήμα, σκεφτήκαμε να συγκρίνουμε την προγνωστική απόδοση των προσαρμοσμένων μοντέλων μας, χρησιμοποιώντας την εκ των υστέρων κατανομή πρόβλεψης της διαφοράς τερμάτων, σε σχέση με τις παρατηρούμενες διαφορές τερμάτων. Πιο συγκεκριμένα, προχωρήσαμε στη σύγκριση των εκ των υστέρων προγνωστικών κατανομών μας (των προσαρμοσμένων μοντέλων) με τις παρατηρούμενες διαφορές γκολ διαγραμματικά μέσω των ραβδογραμμάτων και των 95% διαστημάτων των προγνώσεων (απεικονισμένα με μπάρες σφαλμάτων). Αυτά τα διαγράμματα είναι χρήσιμα, καθώς μπορούμε να απεικονίσουμε πόσο κοντά είναι τα 95% εκ των υστέρων διαστήματα των προβλεπόμενων συχνοτήτων των διαφορών τερμάτων στις αντίστοιχες παρατηρούμενες. Επίσης, στο δεξί μέρος των διαγραμμάτων εμφανίζονται οι τιμές του «Μέσου Απόλυτου Σφάλματος» (Mean Absolute Error, MAE) με την οποία ποσοτικοποιούμε την απόσταση των συχνοτήτων των προβλέψεων από τις παρατηρούμενες συχνότητες για την κάθε τιμή των διαφορών των γκολ.
Με βάση το Διάγραμμα 2, παρατηρούμε ότι όλα τα προσαρμοσμένα μοντέλα παρουσιάζουν παρόμοιες επιδόσεις τόσο όσον αφορά τη γραφική αναπαράσταση όσο και τη τιμή σφάλματος του MAE. Η ομοιότητα μεταξύ των προβλεπτικών επιδόσεων όλων των μοντέλων είναι προφανής από τα αντίστοιχα διαγράμματα, όπου σε όλα αυτά, οι διάμεσοι των προβλέψεων (σκούρα σημεία) είναι κοντά στις παρατηρούμενες συχνότητες. Μια προφανής διαφορά μεταξύ των διαφορετικών προσεγγίσεων είναι ότι το Μοντέλο 1 προβλέπει με αυξημένη πιθανότητα την ισοπαλία (δλδ τη διαφορά τερμάτων ίση με μηδέν) σε σύγκριση με τα Μοντέλα 2 και 3.
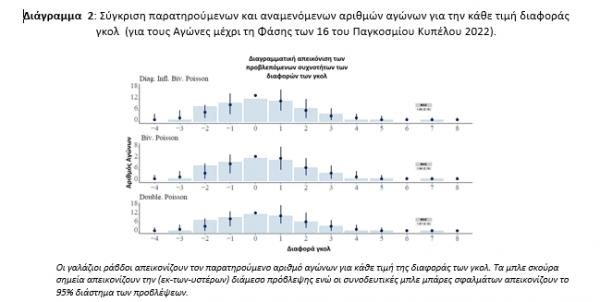
Γενικά, τα αποτελέσματα του Διαγράμματος 2 δείχνουν ότι και τα τρία μοντέλα δίνουν παρόμοιες προβλέψεις με μικρό προβάδισμα στα Μοντέλα 1 και 2. Για το λόγο αυτό επικεντρωθήκαμε περισσότερο στην ανάλυση των δύο πρώτων μοντέλων.
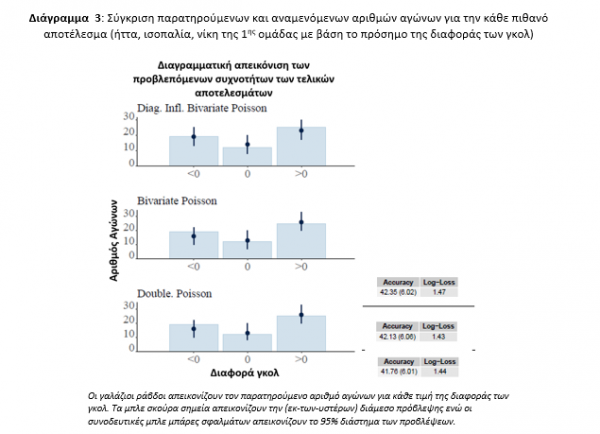
Πιο συγκεκριμένα, οι μικρές διαφορές των αποτελεσμάτων LOO και MAE στο Διάγραμμα 2 μας οδήγησαν να συγκρίνουμε τα μοντέλα μας με βάση την προγνωστική τους απόδοση μόνο για το τελικό αποτέλεσμα του αγώνα χωρίς να λαμβάνουμε υπόψη την ακριβή διαφορά τερμάτων των ομάδων (βλ. Διάγραμμα 3). Δεδομένου ότι τώρα το ενδιαφέρον μας επικεντρώνεται σε τρία πιθανά αποτελέσματα (νίκη της γηπεδούχου ομάδας, ισοπαλία, νίκη της φιλοξενούμενης ομάδας), θα μετρήσουμε την προβλεπτική απόδοση των μοντέλων με βάση δύο δείκτες: (α) την «Ακρίβεια» (accuracy) και (β) τον δείκτη multi-class log-loss (ή αλλιώς multi-class cross entropy – για περισσότερες λεπτομέρειες σχετικά με με αυτό το μέτρο παραπέμπουμε στην ερευνητική εργασία των Grandini, M., et. al, 2020). Αυτό το μέτρο είναι το καταλληλότερο για μοντέλα πρόβλεψης κατηγορικών αποτελεσμάτων, δεδομένου ότι ποσοτικοποιεί πόσο κοντά είναι οι πιθανοθεωρητικές προβλέψεις μας σε σχέση με τα παρατηρούμενα τελικά αποτελέσματα των αγώνων. Τα αποτελέσματα και των δύο αυτών δεικτών δίνονται στο Διάγραμμα 3 μαζί με το αντίστοιχο διάγραμμα των συχνοτήτων των αποτελεσμάτων. Σε αντίθεση με το Διάγραμμα 2, εδώ τα δύο μέτρα υποδεικνύουν ότι το απλούστερο μοντέλο της διμεταβλητής Poisson (δηλαδή το Μοντέλο 2) είναι ελαφρώς καλύτερο από το Μοντέλο 1.
Συμπερασματικά, οι προβλέψεις μας για τους υπόλοιπους αγώνες του Παγκοσμίου Κυπέλλου θα βασίζονται πλέον στο Μοντέλο 2 (Bivariate Poisson). Η συγκεκριμένη αλλαγή στη στρατηγική μοντελοποίησης μας βασίζεται στους ακόλουθους λόγους:
· Το μέτρο LOO-IC ήταν χαμηλότερο (καλύτερο) στο Μοντέλο 2 σε σύγκριση με το Μοντέλο 1.
· Και τα δύο μέτρα προγνωστικής αξιολόγησης στα τελικά αποτελέσματα (Διάγραμμα 3) έδειξαν ως καλύτερη επιλογή μοντελοποίησης το δεύτερο.
· Το απλό διμεταβλητό Poisson είναι απλούστερο από το Μοντέλο 1.
Παρ’ όλα αυτά, ένας αναλυτής θα λάβει παρόμοια αποτελέσματα χρησιμοποιώντας οποιαδήποτε από τα δύο πρώτα μοντέλα για την πρόβλεψη των τερμάτων που σημείωσαν δύο αντίπαλες ομάδες καθώς και για τη διαφορά τερμάτων σε κάθε αγώνα.
Μέχρι το τέλος του τουρνουά, καθώς θα έχουμε όλο και περισσότερους αγώνες στο δείγμα μας, θα προχωρήσουμε σε μια πιο λεπτομερή αξιολόγηση της προβλεπτικής απόδοσης των προσαρμοσμένων μοντέλων χρησιμοποιώντας πρόσθετα προγνωστικά μέτρα.
Βιβλιογραφία για διαβαστερούς φιλάθλους
· Dixon, M.J. and Coles, S.G. (1997), Modelling Association Football Scores and Inefficiencies in the Football Betting Market. Journal of the Royal Statistical Society: Series C (Applied Statistics), 46, 265-280.
· Karlis, D. and Ntzoufras, I. (2003), Analysis of sports data by using bivariate Poisson models. Journal of the Royal Statistical Society: Series D (The Statistician), 52, 381-393.
· Lee A.J. (1997). Modeling Scores in the Premier League: Is Manchester United Really the Best? Chance, 10, 15-19.
· Maher, M.J. (1982), Modelling association football scores. Statistica Neerlandica, 36, 109-118.
· Reep, C., & Benjamin, B. (1968). Skill and Chance in Association Football. Journal of the Royal Statistical Society. Series A (General), 131, 581-585.

Λίγα λόγια για τους Συγγραφείς
O Leonardo Egidi είναι επίκουρος καθηγητής Στατιστικής στο Πανεπιστήμιο της Τεργέστης στην Ιταλία και μέλος της ερευνητικής ομάδας του Οικονομικού Πανεπιστημίου Αθηνών AUEB Sports Analytics Group. Έχει διδακτορικό στην μοντελοποιηση και αναλυτική ποδοσφαίρου και έντονη ερευνητική δραστηριότητα στη Μπευζιανή Στατιστική μεθοδολογία.
O Βασίλης Παλάσκας είναι Στατιστικός Αναλυτής και Επιστήμονας Δεδομένων στην Fantasy Sports Interactive (FSI). Είναι ενεργό μέλος της ερευνητικής ομάδας AUEB Sports Analytics από το 2019 όπου τελείωσε το M.Sc. in Statistics του Οικονομικού Πανεπιστημίου Αθηνών.
O Ιωάννης Ντζουφρας είναι καθηγητής Στατιστικής και πρόεδρος στο Τμήμα Στατιστικής του Οικονομικού Πανεπιστημίου Αθηνών. Είναι ιδρυτικό μέλος της ερευνητικής ομάδας AUEB Sports Analytics Group μαζί με τον Δημήτρη Καρλή. Έχει αναγνωρισμένη επιστημονική δραστηριότητα σε τομείς όπως η Μπευζιανή στατιστική μεθοδολογία, υπολογιστική στατιστική, Βιοστατιστική, ψυχομετρία και αναλυτική των σπορ.
O Δημήτρης Καρλής είναι καθηγητής Στατιστικής και αναπληρωτής πρόεδρος στο Τμήμα Στατιστικής του Οικονομικού Πανεπιστημίου Αθηνών. Είναι ιδρυτικό μέλος της ερευνητικής ομάδας AUEB Sports Analytics Group μαζί με τον Ιωάννη Ντζούφρα. Έχει αναγνωρισμένη επιστημονική δραστηριότητα σε τομείς όπως η στατιστική μεθοδολογία, υπολογιστική στατιστική, Βιοστατιστική, και αναλυτική των σπορ.
Ενεργές Συνεργασίες των Συγγραφέων
Οι τρεις συγγραφείς (L. Egidi, Ι. Ντζούφρας και Δ. Καρλής) του άρθρου αυτή τη στιγμή συνεργάζονται για τη συγγραφή ενός βιβλίου σε Football Analytics σε διεθνή επιστημονικό οίκο ενώ στο τελευταίο workshop της ομάδας έδωσαν ένα σεμιναριακό μάθημα σε Football analytics.
Ο L. Egidi και Β. Παλάσκας συνεργάζονται στην ανάπτυξη του λογισμικού “footbayes” (βιβλιοθήκη της στατιστικής γλώσσας προγραμματισμού R).
Ο L. Egidi, Ι. Ντζούφρας και Β. Παλάσκας συνεργάζονται στην συγγραφή ενός επιστημονικού άρθρου αξιολόγησης παικτών στο Βόλεϊ.
Ο Ι. Ντζούφρας και Β. Παλάσκας συνεπιβλέπουν μια διπλωματική εργασία στα πλαίσια του M.Sc. in Statistics του ΟΠΑ και της συνεργασίας με την FSI (Fantasy Sports Interactive)
Η Ομάδα AUEB Sports Analytics
Η ερευνητική ομάδα του Οικονομικού Πανεπιστημίου Αθηνών AUEB Sports Analytics Group ιδρύθηκε το 2015 από τους καθηγητές Ιωάννη Ντζούφρα και Δημήτρη Καρλή. Μέλη του είναι σημαντικά μέλη της κοινότητα της αναλυτικής των σπορ όπως oι Leonardo Egidi (Πανεπιστήμιο Trieste), Ιωάννης Κοσμίδης (Warwick), Κωνσταντίνος Πελεχρίνης (Pittsburg), Nial Friel (UCD) και Gianluca Baio (UCL) καθώς επίσης και ο πρώην προπονητής της εθνικής Ελλάδας Βόλεϊ, Σωτήρης Δρίκος και ο νυν προπονητής της Εθνικής ομάδας Μπάσκετ του Κοσόβου, Χρήστος Μαρμαρινός. Η ερευνητική ομάδα είναι υπεύθυνη για της σειρά ετήσιων συνεδρίων με το όνομα AUEB Sports Analytics Workshop (6 συνολικά) ενώ το 2019 διοργάνωσε το διεθνές συνέδριο MathSport 2019 με 200 συμμετέχοντες επιστήμονες από όλο τον κόσμο. Η ομάδα έχει μια σειρά από σημαντικές επιστημονικές δημοσιεύσεις στο χώρο της αναλυτικής των σπορ. Τέλος θα θέλαμε να αναφέρουμε ότι η ομάδα ιδρύθηκε το 2015 λόγω της επίσκεψης του καθηγητή Stefan Kesenne (Πανεπιστήμιο Antwerp & Leuven), σπουδαίου Οικονομολόγου του Αθλητισμού που έπαιξε και ενεργό ρόλο στην υπόθεση Bosman. Ο Stefan Kesenne στήριξε ενεργά την ομάδα μέχρι και το 2021 όπου ξαφνικά απεβίωσε. Η ύπαρξη της ομάδας AUEB Sports Analytics Group οφείλεται σε μεγάλο ποσοστό στη συνδρομή και την έμπνευση που μας έδωσε ο κος Kesenne.
* L. Egidi, Β. Παλάσκας, Ι. Ντζούφρας & Δ. Καρλής, Ερευνητική ομάδα AUEB Sports Analytics, Οικονομικό Πανεπιστήμιο Αθηνών, Πανεπιστήμιο της Τεργέστης & Fantasy Sports Interactive
* Συγγραφέας του παρόντος άρθρου είναι ο Ιωάννης Ντζούφρας. Το άρθρο είναι βασισμένο στην ανάλυση των Leonardo Egidi (Πανεπιστήμιο της Τεργέστης) και του Βασίλειου Παλάσκα (Fantasy Sports Interactive) με τις συμβουλευτικές συνδρομές των Ι. Ντζούφρα και Δ. Καρλή. Και οι τέσσερεις συγγραφείς είναι ενεργά μέλη της ερευνητικής ομάδας του Οικονομικού Πανεπιστημίου Αθηνών: AUEB Sports Analytics Group.











![ΦΠΑ: Τι θα συμβεί στο «ράφι» αν μειωθεί ο συντελεστής – Η ανάλυση της ΤτΕ [γραφήματα]](https://www.ot.gr/wp-content/uploads/2025/07/ot_taxes44.png)
![ΤτΕ: Δυναμική ανάπτυξη με υψηλό πληθωρισμό για την Ελλάδα μέχρι το 2027 [πίνακας]](https://www.ot.gr/wp-content/uploads/2025/06/ot_greec_economy799-1024x600-1.png)